Article Peer-Reviewed
Open
Peer Review
Peer Review
Detecting Railway Track Irregularities with Data-driven Uncertainty Quantification
1
Computer Engineering and Networks Laboratory, Information Technology and Electrical Engineering Department, ETH Zürich, 8092 Zürich, Switzerland
2
Department of Applied Mathematics and Computer Science, Technical University of Denmark (DTU), 2800 Kgs. Lyngby, Denmark
*
For correspondence.
Academic Editor:
Received: 21 September 2024 Accepted: 18 February 2025 Published: 7 March 2025
Abstract
This study addresses the critical challenge of assessing railway track irregularities using advanced machine learning techniques, specifically convolutional neural networks (CNNs) and conformal prediction. Leveraging high-fidelity sensor data from high-speed trains, we propose a novel CNN model that significantly outperforms state-of-the-art results in predicting track irregularities. Our CNN architecture, optimized through extensive hyperparameter tuning, comprises multiple convolutional layers with batch normalization, Exponential Linear Unit (ELU) activation functions, and dropout regularization. This design enables the model to capture complex spatial and temporal dependencies in the train’s dynamic responses, translating them into accurate predictions of track irregularities. The model achieves a mean unsigned error of 0.31 mm on the test set, surpassing the previous state-of-the-art performance and approaching industry-standard benchmarks for track measurement accuracy. This level of precision is crucial for the early detection of track defects that could compromise safety and ride quality. To quantify uncertainty in the model’s predictions, we implement conformal prediction techniques, specifically the CV+ and CV-minmax methods. These approaches provide prediction intervals with high reliability, achieving a 97.18% coverage rate for the CV-minmax method. The resulting prediction intervals have an average width of 2.33 mm, offering a balance between precision and confidence in the model’s outputs. Notably, our model exhibits impressive computational efficiency, capable of processing over 2000 kilometers of track data per hour. This speed makes it suitable for real-time applications in continuous monitoring systems, potentially revolutionizing the approach to railway maintenance. The integration of CNNs with conformal prediction represents a significant advancement in the field of predictive maintenance for railway infrastructure. By providing both accurate predictions and well-calibrated uncertainty estimates, our approach enables more informed decision-making in track maintenance planning and safety assessments.
Figures in this Article
Figure 1A
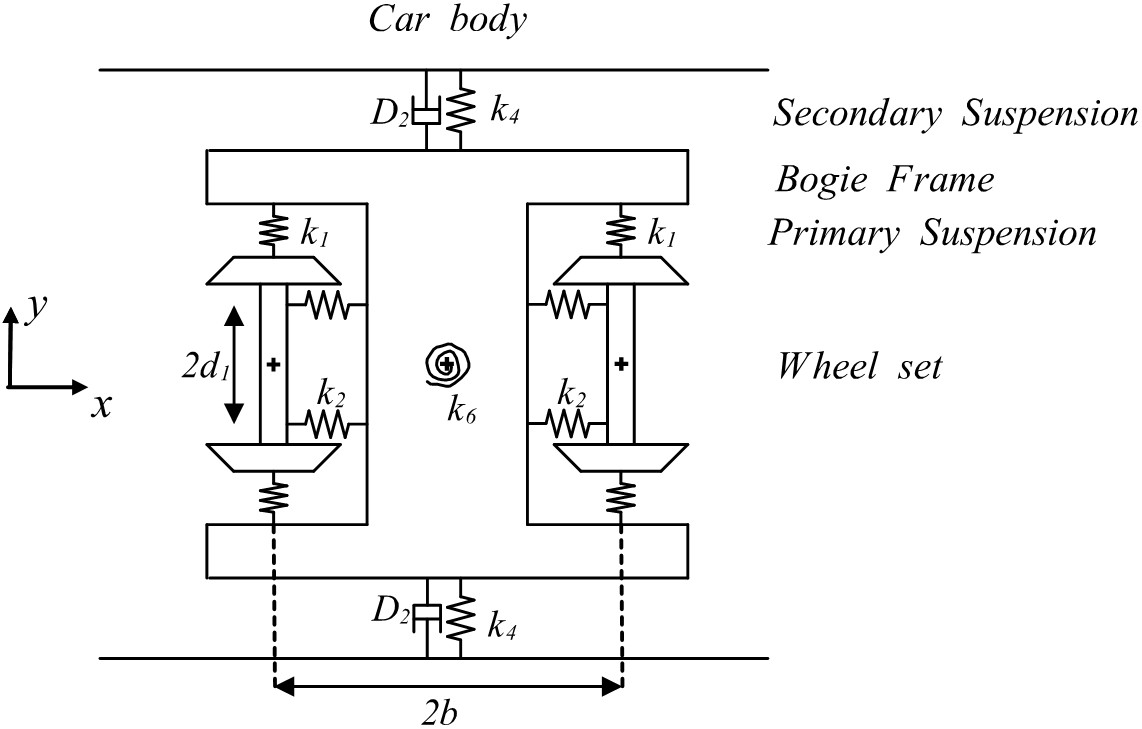Figure 1B
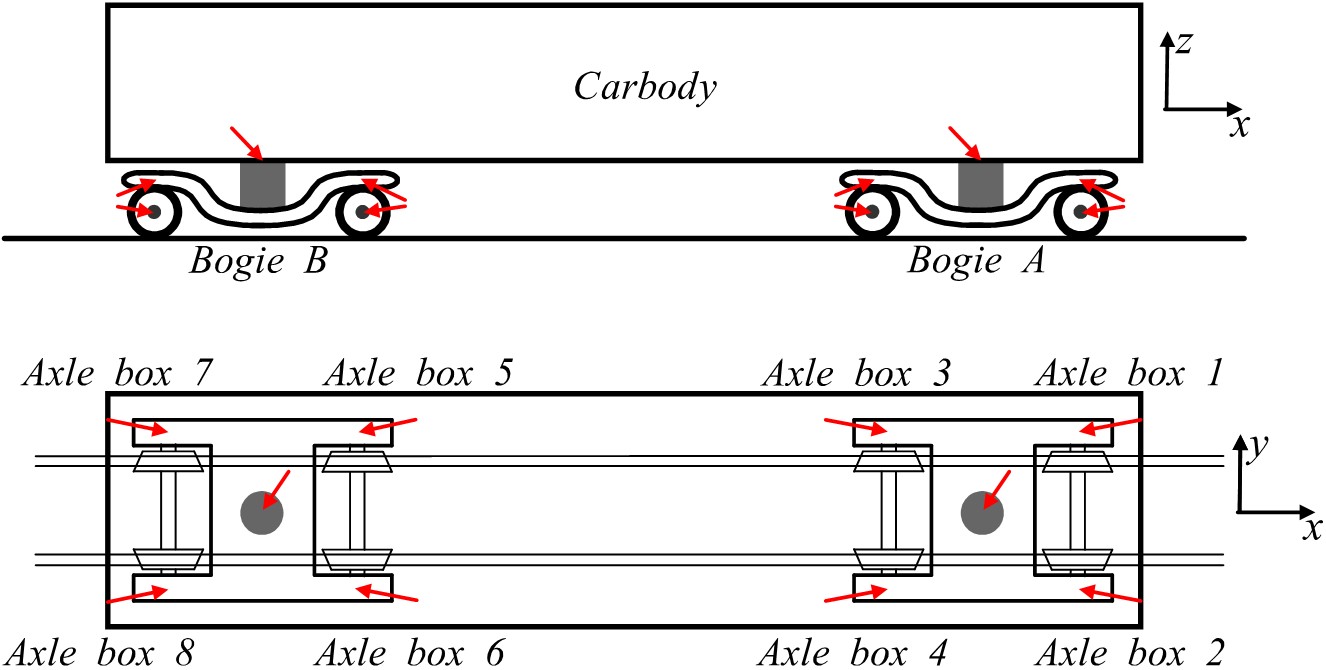Figure 2
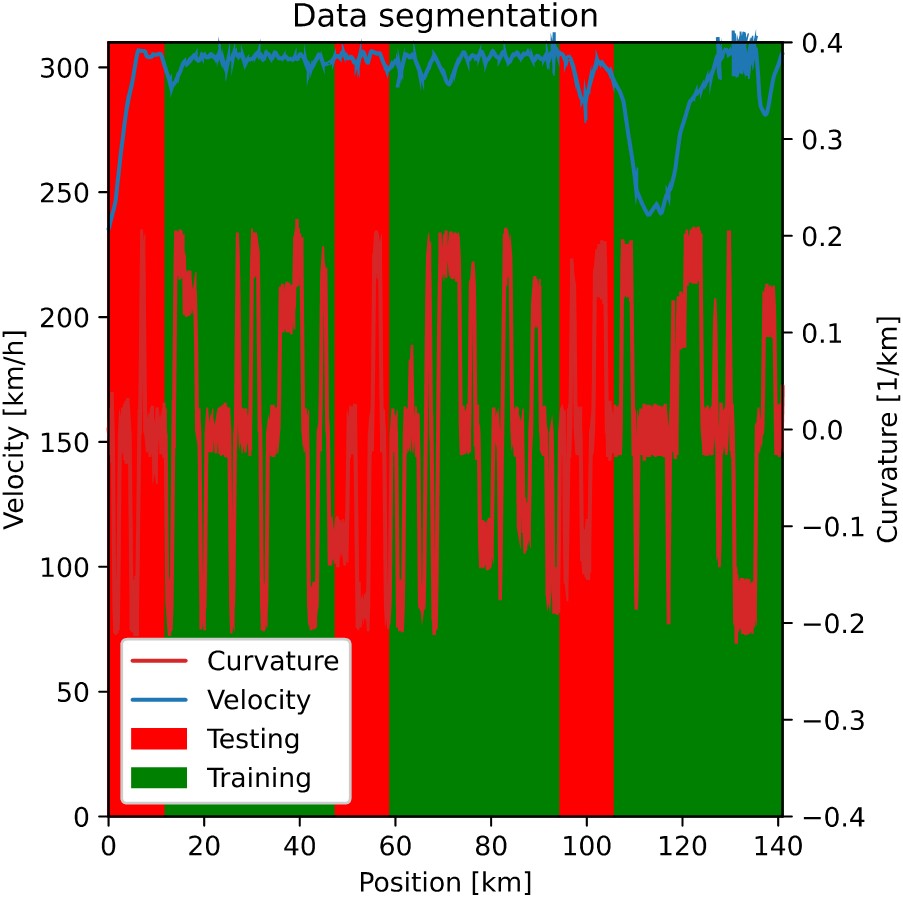Figure 3
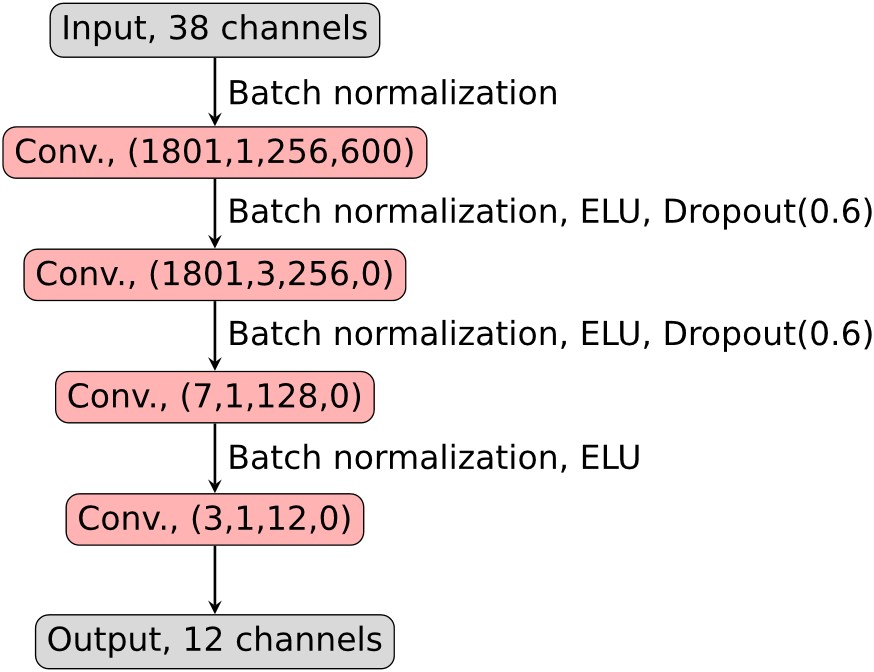Figure 4
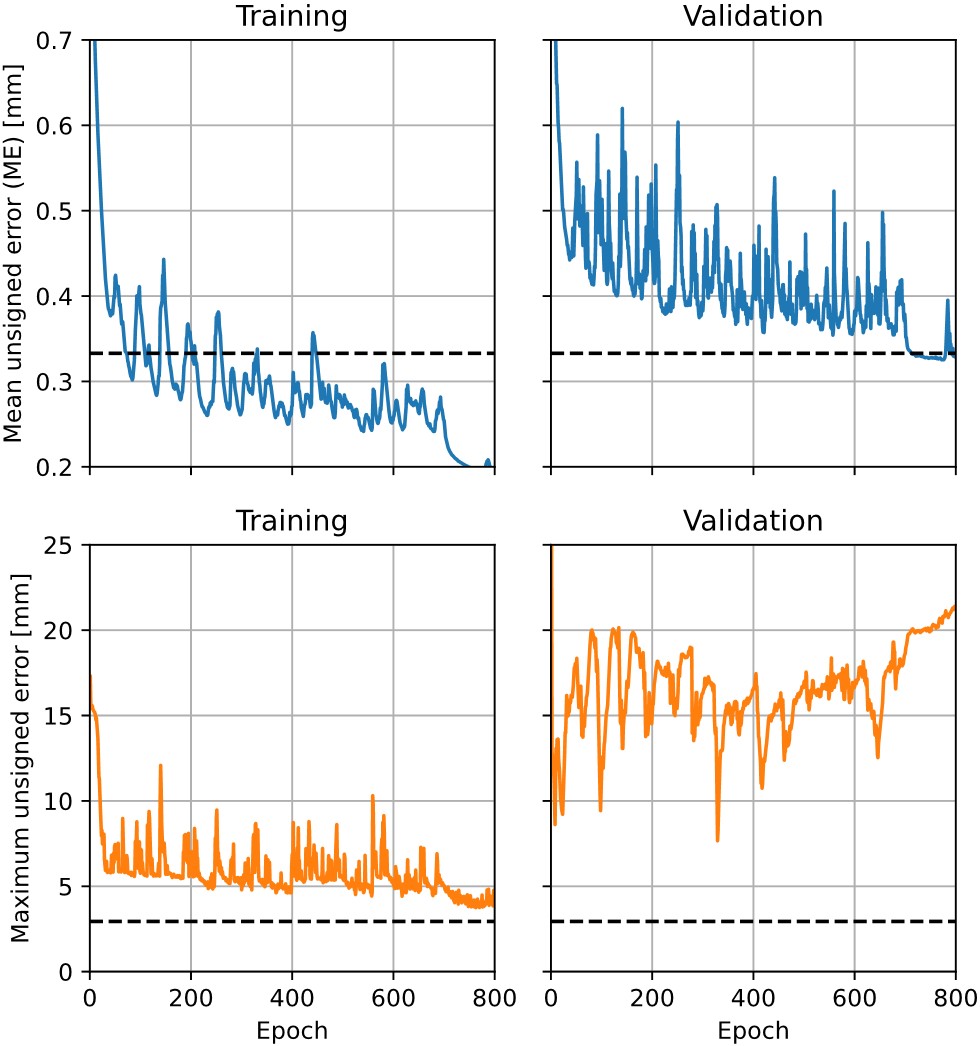Figure 5
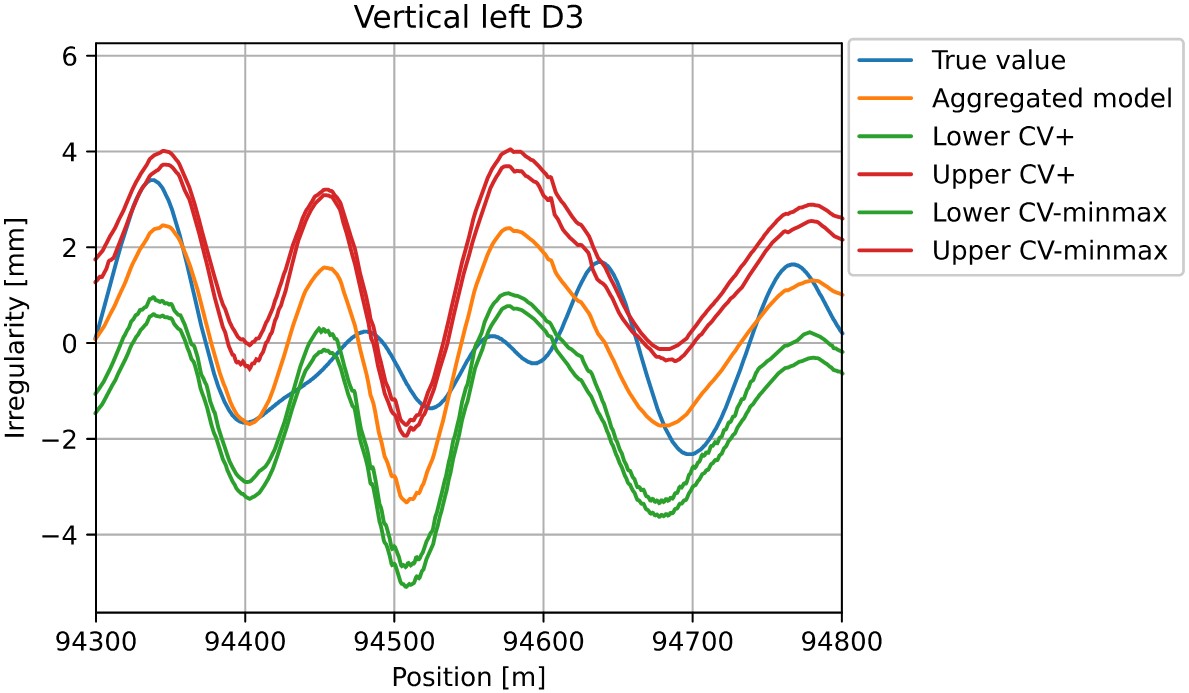Figure 6
Would you like to reuse the images? Contact the journal editorial office to obtain high-quality versions.
Keywords
railway track integrity; convolutional neural networks; conformal prediction; predictive maintenance; sensor data analysis; machine learning; uncertainty quantification
Copyright © 2025
Plesner et al. This article is distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use and distribution provided that the original work is properly cited.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Cite this Article
Plesner, A., Engsig-Karup, A. P., & True, H. (2025). Detecting Railway Track Irregularities with Data-driven Uncertainty Quantification. Highlights of Vehicles, 3(1), 1–14. https://doi.org/10.54175/hveh3010001
References
1.
Plesner, A., Engsig-Karup, A. P., & True, H. (2024). Detecting railway track irregularities using conformal prediction. In Proceedings of the 33rd International Conference on Artificial Neural Networks. Springer, Cham.
2.
European Committee for Standardization. (2017). En CEN 13848-5, railway applications–track–track geometry quality–part 5: geometric quality levels–plain line, switches and crossings.
3.
Kawasaki, J., & Youcef-Toumi, K. (2002). Estimation of rail irregularities. Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), 5, 3650–3660. https://doi.org/10.1109/acc.2002.1024495
4.
Hao, X., Yang, J., Yang, F., Sun, X., Hou, Y., & Wang, J. (2023). Track geometry estimation from vehicle–body acceleration for high-speed railway using deep learning technique. Vehicle System Dynamics, 61(1), 239–259. https://doi.org/10.1080/00423114.2022.2037669
5.
Ravitharan, R. (2019). Safer rail operations: Reactive to proactive maintenance using state-of-the-art automated in-service vehicle-track condition monitoring. In Proceedings of the 2018 International Conference on Intelligent Rail Transportation. IEEE. https://doi.org/10.1109/ICIRT.2018.8641587
6.
Weston, P., Roberts, C., Yeo, G., & Stewart, E. (2015). Perspectives on railway track geometry condition monitoring from in-service railway vehicles. Vehicle System Dynamics, 53(7), 1063–1091. https://doi.org/10.1080/00423114.2015.1034730
7.
Lee, J. S., Choi, S., Kim, S. S., Kim, Y. G., Kim, S. W., & Park, C. (2012). Waveband analysis of track irregularities in high-speed railway from on-board acceleration measurement. Journal of Solid Mechanics and Materials Engineering, 6(6), 750–759. https://doi.org/10.1299/jmWWmp.6.750
8.
Balouchi, F., Bevan, A., & Formston, R. (2021). Development of railway track condition monitoring from multi-train in-service vehicles. Vehicle System Dynamics, 59(9), 1397–1417. https://doi.org/10.1080/00423114.2020.1755045
9.
Chudzikiewicz, A., Bogacz, R., Kostrzewski, M., & Konowrocki, R. (2018). Condition monitoring of railway track systems by using acceleration signals on wheelset axle-boxes. Transport, 33(2), 555–566. https://doi.org/10.3846/16484142.2017.1342101
10.
Muñoz, S., Ros, J., Urda, P., & Escalona, J. L. (2021). Estimation of lateral track irregularity through kalman filtering techniques. IEEE Access, 9, 60010–60025. https://doi.org/10.1109/ACCESS.2021.3073606
11.
Muñoz, S., Ros, J., Urda, P., & Escalona, J. L. (2021). Estimation of lateral track irregularity using a kalman filter. experimental validation. Journal of Sound and Vibration, 504, 116122. https://doi.org/10.1016/j.jsv.2021.116122
12.
Naganuma, Y., Kobayashi, M., & Okumura, T. (2010). Inertial measurement processing techniques for track condition monitoring on shinkansen commercial trains. Journal of Mechanical Systems for Transportation and Logistics, 3(1), 315–325. https://doi.org/10.1299/jmtl.3.315
13.
Tsunashima, H., & Hirose, R. (2022). Condition monitoring of railway track from car-body vibration using time–frequency analysis. Vehicle System Dynamics, 60(4),1170–1187. https://doi.org/10.1080/00423114.2020.1850808
14.
Wei, X., Liu, F., & Jia, L. (2016). Urban rail track condition monitoring based on in-service vehicle acceleration measurements. Measurement, 80, 217–228. https://doi.org/10.1016/j.measurement.2015.11.033
15.
Aslam, Y., & Santhi, N. (2019). A review of deep learning approaches for image analysis. In Proceedings of the 2019 International Conference on Smart Systems and Inventive Technology (ICSSIT) (pp. 709–714). IEEE. https://doi.org/10.1109/ICSSIT46314.2019.8987922
16.
O’Mahony, N., Campbell, S., Carvalho, A., Harapanahalli, S., Hernandez, G. V., Krpalkova, L, et al. (2020). Deep learning vs. traditional computer vision. In Advances in Computer Vision, Proceedings of the 2019 Computer Vision Conference (CVC) (pp. 128–144). Springer, Cham. https://doi.org/10.1007/978-3-030-17795-9_10
17.
Mittal, S., & Rao, D. (2017). Vision based railway track monitoring using deep learning. arXiv. https://doi.org/10.48550/arXiv.1711.06423
18.
De Rosa, A., Kulkarni, R., Qazizadeh, A., Berg, M., Gialleonardo, E. D., Facchinetti, A., et al. (2021). Monitoring of lateral and cross level track geometry irregularities through onboard vehicle dynamics measurements using machine learning classification algorithms. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 235(1), 107–120. https://doi.org/10.1177/0954409720906649
19.
Tsunashima, H. (2019). Condition Monitoring of Railway Tracks from Car-Body Vibration Using a Machine Learning Technique. Applied Sciences, 9(13), 2734. https://doi.org/10.3390/app9132734
20.
Yang, C., Sun, Y., Ladubec, C., & Liu, Y. (2021). Developing Machine Learning-Based Models for Railway Inspection. Applied Sciences, 11(1), 13. https://doi.org/10.3390/app11010013
21.
Li, C., He, Q., & Wang, P. (2021). Estimation of railway track longitudinal irregularity using vehicle response with information compression and Bayesian deep learning. Computer-aided Civil and Infrastructure Engineering, 37(10), 1260–1276. https://doi.org/10.1111/mice.12802
22.
Varona, B., Monteserin, A., & Teyseyre, A. (2020). A deep learning approach to automatic road surface monitoring and pothole detection. Personal and Ubiquitous Computing, 24, 519–534. https://doi.org/10.1007/s00779-019-01234-z
23.
Plesner, A. (2022). Using data-driven state-of-the-art machine learning and conformal prediction for track irregularities from observed dynamics of inservice railway vehicles [Master’s Thesis]. Technical University of Denmark.
24.
True, H., Christiansen, L. E., Plesner, A. L., Ammitzbøll, A. L., & Dahl, B. J. (2020). Why is it so difficult to determine the lateral position of the rails by a measurement of the motion of an axle on a moving vehicle? In Second International Conference on Rail Transportation. Southwest Jiaotong University.
25.
True, H., Christiansen, L. E., Plesner, A. L., Ammitzbøll, A. L., & Dahl, B. J. (2023). On the problem of the dynamical reactions of a rolling wheelset to real track irregularities. Railway Engineering Science, 31(1), 1–19. https://doi.org/10.1007/s40534-022-00288-9
26.
Cai, S., Mao, Z., Wang, Z., Yin, M., & Karniadakis, G. E. (2021). Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mechanica Sinica, 37(12), 1727–1738. https://doi.org/10.1007/s10409-021-01148-1
27.
Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., & Yang, L. (2021). Physics-informed machine learning. Nature Reviews Physics, 3(6), 422–440. https://doi.org/10.1038/s42254-021-00314-5
28.
Markidis, S. (2021). Physics-informed deep-learning for scientific computing. arXiv. https://doi.org/10.48550/arXiv.2103.09655
29.
Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2017). Physics informed deep learning (Part I): Data-driven solutions of nonlinear partial differential equations. arXiv. https://doi.org/10.48550/ARXIV.1711.10561
30.
Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707. https://doi.org/10.1016/j.jcp.2018.10.045
31.
Clevert, D. A., Unterthiner, T., & Hochreiter, S. (2020). Fast and accurate deep network learning by exponential linear units (ELUs). arXiv. https://doi.org/10.48550/arXiv.1511.07289
32.
Ioffe, S., & Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (Vol. 37, pp. 448–456). JMLR.
33.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929–1958.
34.
Balasubramanian, V., Ho, S. S., & Vovk, V. (2014). Conformal prediction for reliable machine learning: theory, adaptations and applications. Elsevier. https://doi.org/10.1016/C2012-0-00234-7
35.
Barber, R. F., Candes, E. J., Ramdas, A., & Tibshirani, R. J. (2021). Predictive inference with the jackknife+. The Annals of Statistics, 49(1), 486–507. https://doi.org/10.1214/20-AOS1965
36.
Shafer, G., & Vovk, V. (2008). A tutorial on conformal prediction. Journal of Machine Learning Research, 9, 371–421.
37.
Vovk, V., Gammerman, A., & Shafer, G. (2005). Algorithmic learning in a random world. Springer. https://doi.org/10.1007/b106715
Metrics
Loading...
Journal Menu
Journal Contact
Highlights of Vehicles
Editorial Office
Highlights of Science
Avenida Madrid, 189-195, 3-3
08014 Barcelona, Spain
08014 Barcelona, Spain
Jene Zhang
Managing Editor
